n  一些大原则：

─ 认定能够实际接触到的母群体，也就是抽样架构（sampling frame）。

─ 避免随意抽样（亦即非机率性的抽样）。

─ 理想上是能做简单随机抽样或系统抽样。

─ 分层抽样可以减少抽样误差。

─ 当母群体中每一位被抽样的对象是分属于某一团体时，则可考虑用随机丛集抽样（cluster sampling）。

─ 当母群体很大时，应考虑用多阶段抽样。

─ 决定样本的大小是以推估母数（parameter）时所欲达到之精准度为基础。

─ 大样本并不能补偿抽样时的偏差或系统性偏差（sampling bias；systematic bias）。因此，良好的抽样设计、问卷设计和增加回收率等都是减少偏差的重要步骤。

n  在抽样方面，需要做以下之判断及决策:

─ 是否要用机率样本（probability sample，亦即random sample）？

─ 抽样架构(the sampling frame)为何？也就是那些人真正有被抽选到之机会。

─ 样本之大小(The Sample Size)。

─ 抽样设计(the sample design)，即抽选人或户之实际策略。

─ 回收率(the rate of response)，即真正得到数据者在选取样本中之比例。

n  样本之选取的三个关键

─ 得到样本时所用之the sample frame(样本架构)。

─ 样本内每一单位或个案都必须是用机率抽样之程序，获得每一个单位都应知道被选取之机率为何。

─ 抽样设计之细节，如样本大小，及抽样程序等，都会影响到样本之代表性。

n  The Sample Frame

任何一个选择样本之程序都会给一些人被选入样本之机会，也同时会排除一些人。因此，第一个评估样本质量之步骤即为了解the sample frame 。

─ 抽样方法可以归成三大类:

（1）          抽样是由一相当完整的名单中抽出样本。

（2）          抽样是由一群因做某些事或到某些地方的人中抽出样本。

（3）          抽样是透过几个阶段抽到样本。

─ 不论抽样方法为何，研究者要评估the sample frame 之三个特征:

（1）  包含性(comprehensiveness)与变异性（variation）。

（2）  样本中每一个人或单位都有已知之被选择的机率。

（3）  最后一个评估的标准是抽样设计之效率(efficiency)。这标准主要牵涉到抽样所需之成本效益的问题。

    由于样本推论之范围限于the sample frame，因此研究者要报告什么人有机会被选择，什么人被排在外，那些被排在外的是否有独特之性质，以及是否有些被抽选者其被抽选之机率不明等。

n  一个阶段的抽样

─ 简单随机抽样：将抽样架构中所有的元素编号后，再用一组随机数决定挑选哪些元素。

─ 系统抽样：将抽样架构中每一个元素编号，但不用随机数选取，而是依照一定的抽样间距。

─ 分层抽样：将母群体分成几个次母群体（subpopulation）的分层（strata）后，从每个次母群体中抽出一定比例的随机样本。

n  多阶段抽样

 ─ 由学校中抽选学生

 ─ 区域机率抽样(Area Probability Sampling)

 ─ 随机数字拨号(random-digit dialing)

n  样本推估及抽样误差

一般来说，随机抽样所得到的误差假定为非系统性的偏差，因此我们可以推估样本估计值之准确性。(您还记得the central limit theorem吗?)

以下所谈之原则虽是运用在所有的sample statistics，但是一般的estimates主要是means（平均数）。最常用来描述抽样误差之统计值即为标准误差(standard error)，透过标准误差我们可以计算信赖区间。

平均数之standard error 为 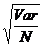  ， Var为样本之变异量；

比例之SE为 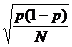   ， p (1-p)为比例之变异量。

由以上公式可看出:

─ 样本愈大，则抽样误差愈小。

─ 当原来样本数小时，加大样本数，会减少较多之误差，但原样本颇大时，加多样本数能减少之误差并不大。

─ 当p = 0.5时，比例之抽样误差最大。

─ 上述之公式只用在simple random sample之情况。当抽样不是简单随机时，样本误差之计算会随设计之不同而不同，也会随所注意之变项不同而不同。

─ 上述之标准误差只和抽样之过程有关，并非涵盖所有其它调查过程中所产生之别种误差(如个别受访者可能造成之误差)。

n  样本大小之决定

样本大小的决定是看：

─ 信赖区间的大小，也就是容许type I error或α的大小（如α = 0.05）

─ 希望利用样本值在推估母数时能有的精确程度

─ 对一些母数最合理的猜测

例如以是否投给某位候选人的调查为例，因答项只有两个（是或否），而以推估回答「是」之比例（p）的精确度（如在±0.03），且在95％信赖区间的条件下来决定样本大小：

则我们希望p ±0.03；此0.03和95％信赖区间的关系是：

p ±0.03       p ±1.96

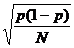
也就是 0.03 = 1.96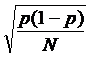

既然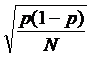最大时为p = 0.5时，最保守的作法是将p = 0.5放入公式中计算，会得到 = 。

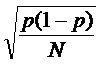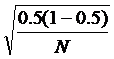因此如何使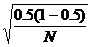 = 0.03就是要解的方程式。答案是N = 1067.11。

以上面的情况为基准（即α = 0.05，p = 0.5），当

精确程度为                        估计需要的样本数为

   ± 10％                                         100

    ±  7％                                           200

    ±  5％                                           400

    ±  3％                                           1000

    ±  2％                                           2400

    ±  1％                                           9600

以上讨论是在简单随机抽样的基础上，如果不是简单随机抽样，需有其他的考虑，如利用丛集抽样所得到同样大小的样本，其有效样本数（effective sample size）事实上较少。

n  未回答或回收所造成的偏差

机率样本之原则是母群体中每一个人都有一已知之抽选机率，因此样本数据之质量即受到真正收集到数据的样本与原预定样本间比例即回收率之影响。在此所要讨论之未回答（Nonresponse）是指那些完全无法得到资料之情况，而不是调查问卷中有些人未回答一些问题之情况。

一般说来，有三种理由无法自一些预定之对象中获得数据:

─ 数据收集之方法或步骤无法联络或找到受访者，因此根本没机会让他们回答问题。

─ 受访者拒绝提供数据。

─ 受访者没有能力回答，如生病，不会听、说访问者所用之语言，或无读写之能力，以致无法回答自填之问卷。

未回答之情况最重要的影响是可能使最后所得到之样本与原来之母群有系统性之差异而造成 bias，此和前述之 Sampling error有所不同。

n  未回答所造成之偏差

未回答者对于样本推估所造成之影响要看未回收之比例以及未回答者在何者程度上和母群有系统性之差异而定。

   以母群体要投某位候选人之真正比例是25％为例，当回收率为90％，而未回收者中有25％的人会投此候选人的话，则样本得到的比例自然会在25％左右；但当未回收者中只有10％会投此候选人，则得到的比例会在27％左右（倾向高估）；而当未回收者中有75％会投此候选人，则得到的比例会在19％左右（倾向低估）。

当回收率为70％，而未回收者中有25％的人会投此候选人的话，则样本得到的比例自然也会在25％左右；但当未回收者中只有10％会投此候选人，则得到的比例会在31％左右（倾向高估）；而当未回收者中有75％会投此候选人，则得到的比例会在3％左右（严重低估）。所以当回收率是在70％以下时，我们要对其得到的结果十分小心。

n  增加回收率之办法

在电话或访问调查方法时，通常要处理两个造成无法回收之问题，一为接触到受访者，另一为得到合作。对前一个问题，通常采取以下两方法：

─ 多次造访，特别是在晚上或周末，造访所需之次数视状况而定，在都会地区，一般言至少要6次。电话调查因成本较低，故一般要求是打10次。

─ 要求访员访问之时间有弹性，以便和受访者约一方便受访者之时间。

在征得合作方面，通常有下列做法:

─ 如果可能的话，应先寄一含相当详尽介绍调查内容之信，如此可使一些受访者没有疑虑，亦可使访员较有信心。

─ 有效且正确的告诉受访者调查之目的。让受访者感到其帮助之重要。

─ 让受访者放心其回答不会使其受到危险或感胁。

─ 有效率之访员。要使访员知道回收率高之重要性。要能迅速发现回收率方面之问题。并停用无效率之访员。

n  质性研究的抽样设计

─ 重视从理论的基础出发，寻找有丰富信息内涵的个案。

─ 抽样架构：可以地点、事件、人、活动、时间等来分类。

─ 抽样策略：